ntegral adalah kebalikan dari proses diferensiasi. Integral ditemukan menyusul ditemukannya masalah dalam diferensiasi di mana matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi. Lambang integral adalah 
Integral terbagi dua yaitu integral tak tentu dan integral tentu. Bedanya adalah integral tertentu memiliki batas atas dan batas bawah. Integral tertentu biasanya dipakai untuk mencari volume benda putar dan luas.

Mencari nilai integral
Substitusi
- Contoh soal:
- Cari nilai dari:
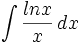
Integrasi parsial
- Integral parsial menggunakan rumus sebagai berikut:
- Contoh soal:
- Cari nilai dari:

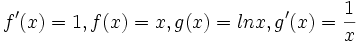
- Gunakan rumus di atas
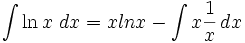
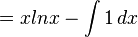

Substitusi trigonometri
| Bentuk | Gunakan |
 |  |
 | 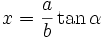 |
 |  |
- Contoh soal:
- Cari nilai dari:

- Cari nilai dari:
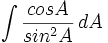 dengan menggunakan substitusi
dengan menggunakan substitusi 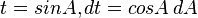
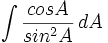
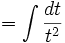
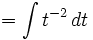
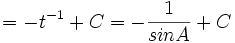
- Cari nilai dari:
- Masukkan nilai tersebut:
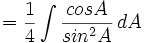
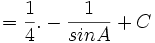

- Nilai sin A adalah



- Nilai sin A adalah
Integrasi pecahan parsial
- Contoh soal:
- Cari nilai dari:

- Akan diperoleh dua persamaan yaitu
 dan
dan 
- Dengan menyelesaikan kedua persamaan akan diperoleh hasil
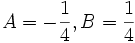
Rumus integrasi dasar
Umum
 (n ≠ -1)
(n ≠ -1)![\int\frac{d}{dx}[f(x)]\,dx = f(x) + C\,](http://upload.wikimedia.org/math/4/1/b/41bcfd2fc1bd9fb1cdc99d54e0a7e7b0.png)

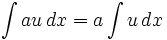 (a adalah konstanta)
(a adalah konstanta)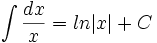
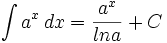 (a > 0, a ≠ 1)
(a > 0, a ≠ 1)






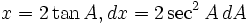

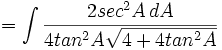


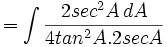
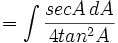

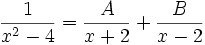

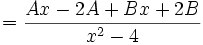
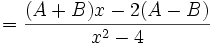


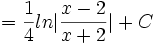



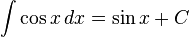
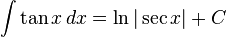
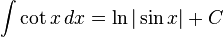


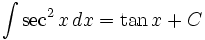

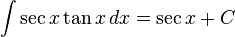

 untuk anda yang telah memasang banner ini, pasti akan saya backlink lagi.. :)
bisa lihat dibawah, anda boleh mencantumkan blog anda sepuasnya..
untuk anda yang telah memasang banner ini, pasti akan saya backlink lagi.. :)
bisa lihat dibawah, anda boleh mencantumkan blog anda sepuasnya..









0 komentar:
Posting Komentar